A. Kelishilgan tushlik
Xotira: 16 MB, Vaqt: 1000 msAli va Vali aka-ukalardir. Ular anchadan beri ko‘rishishmagani sababli, bugun birga tushlik qilishga qaror qilishdi. Qo‘ng‘iroqlashib qayerda tushlik qilishlarini kelishib olishdi. Hozirda Vali tushlik joyidan \(A\) metr uzoqlikda, Ali esa \(B\) metr uzoqlikda joylashgan. Ikkisi ham bir xil tezlik bilan harakat qilishsa, tushlik joyiga kim birinchi yetib boradi?
Agar ikkisi ham bir vaqtda yetib kelishsa \(Same\) deb chiqaring.
Birinchi qatorda bitta butun son - \(A(1 ≤ A ≤ 10^9)\) kiritiladi.
Ikkinchi qatorda bitta butun son - \(B(1 ≤ B ≤ 10^9)\) kiritiladi.
Kelishilgan joyga birinchi keluvchi odam ismini chiqaring. Ikkisi ham bir vaqtda kelsa, \(Same\) deb chiqaring.
.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 4 |
Vali |
| 2 |
5 5 |
Same |
| 3 |
40 35 |
Ali |
B. Massiv bahosi
Xotira: 16 MB, Vaqt: 1000 msSonlardan iborat uzunligi \(m\) bo‘lgan \(c\) massivning bahosi \(c[i] ≠ c[i + 1] (1 ≤ i ≤ m − 1)\) larni qanoatlantiruvchi \(i\) lar soniga teng. Misol uchun [1,3,3, − 1] massivning bahosi 2 ga teng; [7,7] massivning bahosi esa 0 ga teng.
Sizga sonlardan iborat uzunligi \(n\) bo‘lgan \(a\) massiv beriladi. Siz 1 amalda shu massivdagi istalgan ikkita elementlarni tanlab, joylarini almashtirishingiz mumkin. Siz bu amalni cheksiz ko‘p marta bajarsangiz bo‘ladi. Umuman bajarmasangiz ham bo‘ladi.
Sizning vazifaningiz tepadagi amaldan istalgancha bajarib, \(a\) massiv bahosini iloji boricha kichraytirishdir. Hosil bo‘lgan massivni chiqaring. Agar \(a\) massiv bahosi minimal bo‘ladigan natijaviy massivlar bir necha xil bo‘lsa, istalganini chiqaring.
Birinchi qatorda bitta natural son - \(n\) kiritiladi.
Ikkinchi qatorda \(n\) butun son - \(a\) massiv elementlari kiritiladi.
Barcha kiruvchi sonlar modul jihatidan 1000 dan oshmaydi.
Tepada amaldan istalgancha bajargan holda \(a\) massiv bahosini minimallashtiring. Natijaviy massivni chiqaring. Agar natijaviy massiv bir necha xil bo‘lsa, istalganini chiqaring.
1-testda, \(a\) massivning boshlang‘ich bahosi 4 ga teng. 3- va 4- elementlarning joylarini almashtirib \(a\) massiv bahosini 3 gacha tushirish mumkin. Bu erishish mumkin bo‘lgan eng minimal baho ekanligini isbotlasa bo‘ladi. Bu natijaga boshqa usul bilan ham erishsa bo‘lardi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 1 3 4 3 2 |
1 3 3 4 2 |
| 2 |
8 9 1 -3 7 -9 7 -3 12 |
7 7 9 -9 -3 -3 1 12 |
C. Ajoyib kesik matritsa
Xotira: 64 MB, Vaqt: 1000 msKesik matritsa deb ikki qarama qarshi burchagi qirqilgan matritsaga aytiladi. Bunda eni yoki bo‘yi 1 ga teng kesik matritsa mavjud emas. To‘liqroq tushunish uchun quyidagi rasmlarga qarang.
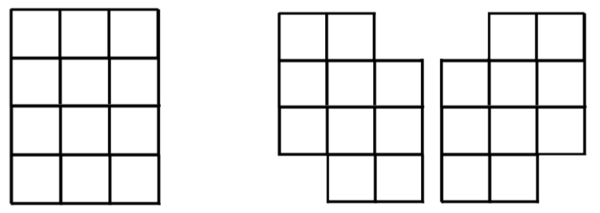
Chapda odatiy matritsa, o‘ngda esa kesik matritsalarga misol keltirilgan.
Kesik matritsaning qirqilmay qolgan ikkita burchagi bir xil sonlardan iborat bo‘lsa, u ajoyib kesik matritsa hisoblanadi.
Asilbekda bo‘yi \(N\) va eni \(M\) bo‘lgan natural sonlardan iborat matritsa bor. Endi u matritsadan ajoyib kesik matritsa kesib olmoqchi. U necha xil usulda buni qila oladi?
Birinchi qatorda ikkita son - \(N\) va \(M\) kiritiladi.
Keyingi \(N\) ta qatorning har birida \(M\) tadan son - Asilbekning matritsasi kiritiladi. Barcha sonlar 500 dan oshmaydigan natural sonlardir.
Asilbek qirqib olishi mumkin bo‘lgan ajoyib kesik matritasalar sonini chiqaring.
1-testdagi Asilbekning matritsasi:
U quyidagicha ajoyib kesik matritsalarni qirqib olishi mumkin:
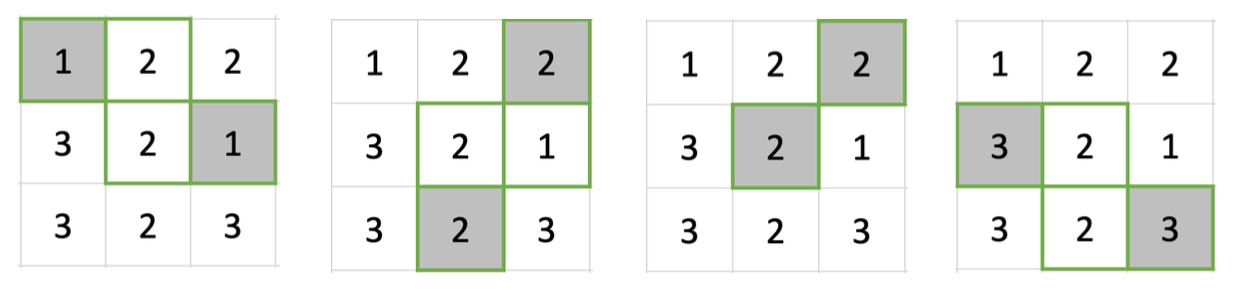
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 1 2 2 3 2 1 3 2 3 |
4 |
| 2 |
3 4 9 2 5 2 5 5 5 9 2 2 5 9 |
9 |
D. Amallarni joylashtirish
Xotira: 32 MB, Vaqt: 1000 msAsilbekka bugun maktabda bir masala berishdi:
1 2 3 4 5 6 7 8 9 = 10
Bu sonlar orasiga +,– amallaridan birini joylashingiz yoki hech qanday amalni joylamasligingiz mumkin. Tenglikni to‘g‘ri qilishning necha xil usuli bor? Hech qanday amal qo‘ymaslik, raqamlarni birlashtirishni anglatadi. Misol uchun, barcha oraliqlar bo‘sh qoldirilsa 123456789 soni hosil bo‘ladi. 1 va 10 sonlarining chap yoniga bironta amal qo‘yish mumkin emas.
Afsuski, Asilbek masalani ishlay olmadi, chunki u dasturchi va qo‘lda hisoblashni umuman yoqtirmaydi. Shuning uchun u uyiga kelib shu masalani ishlovchi dastur tuzdi. Faqat bu safar u 10 ning o‘rniga \(x\) sonini qo‘yib ishladi.
Asilbek buni uddaladi. Sizchi, uddalay olasizmi?
Yagona qatorda bitta butun son - \(x(1 ≤ x ≤ 123456789)\) kiritiladi.
\(1 \ 2 \ 3 \ 4 \ 5 \ 6 \ 7 \ 8 \ 9 = x\). Bu raqamlar orasiga +,– belgilaridan birini yoki hech qanday amal joylamaslik orqali tenglikni to‘g‘ri qilishning usullari sonini chiqaring.
1-testda, 8 hosil qilishning quyidagicha usullari mavjud.
1)1 − 23 + 4 − 56 − 7 + 89 = 8
2)12 + 3 − 4 − 5 − 6 + 7 − 8 + 9 = 8
3)12 − 3 + 4 − 5 + 6 − 7 − 8 + 9 = 8
4)1 − 23 − 45 + 6 + 78 − 9 = 8
5)12 − 3 + 4 − 5 − 6 + 7 + 8 − 9 = 8
6)12 − 3 − 4 + 5 + 6 − 7 + 8 − 9 = 8
7)12 + 3 + 4 + 5 − 6 + 7 − 8 − 9 = 8
8)1 − 2 + 34 + 5 − 6 − 7 − 8 − 9 = 8
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
8 |
8 |
| 2 |
123456789 |
1 |
| 3 |
10 |
12 |
E. Darvozalarni qo'riqlash
Xotira: 64 MB, Vaqt: 2500 msYaqindagina juda katta “DataToMoney” banki barpo etildi. Bu bank shunchalar kattaki, unda \(N\) ta darvozasi mavjud. Hali yangi bo‘lgani uchun hozircha bankning hech qaysi darvozasida qo‘riqchilar joylashtirilmagan.
Bank direktori \(Q\) marta quyidagi ikki xil so‘rovdan birini berishi mumkin.
- Birinchi turdagi so‘rov: \([l…r]\) oraliqdagi barcha darvozalarga lavozimi\(v\) bo‘lgan yangi qo‘riqchini tayinlash. Bunda shu oraliqdagi biron darvozalarni boshqa qo‘riqchi nazorat qilayotgan bo‘lsa, bu qo‘riqchi boshqa bu darvozani nazorat qilmasin.
- Ikkinchi turdagi so‘rov: eng zaif qo‘riqlanayotgan darvozalar sonini aytishingiz kerak bo‘ladi. \(i\)-darvoza \(j\)-darvozadan zaifroq qo‘riqlanadi, agar \(i\)-darvozani nazorat qiluvchi qo‘riqchi lavozimi, \(j\)-darvozani qo‘riqlovchi darvoza qo‘riqchisi lavozimidan kichikroq bo‘lsa, yoki \(j\)-darvoza qo‘riqlanib \(i\)-darvoza umuman qo‘riqlanmasa.
Siz direktorning so‘rovlarini bajaruvchi dastur tuzing. Bunda faqatgina 2-turdagi so‘rov uchun eng zaif qo‘riqlanayotgan darvozalar sonini chiqaring.
2-turdagi so‘rovdan kamida bitta berilishi kafolatlanadi.
Birinchi qatorda ikkita butun son - \(N, Q(1 ≤ N, Q ≤ 2 * 10^5 )\) bankdagi darvozalar va direktorning so‘rovlari soni.
Keyingi \(Q\) ta qatorning har birida so‘rovni turini ifodalovchi \(t ∈ [1,2]\) kiritiladi. Agar \(t=2\)bo‘lsa, demak so‘rov ikkinchi turda. Agar \(t = 1\) bo‘lsa so‘rov birinchi turda, hamda qo‘shimcha tarzda \(l, r, v(1 ≤ l ≤ r ≤ N, 1 ≤ v ≤ 10^9)\)lar kiritiladi.
Har bir 2-turdagi so'rov uchun alohida qatorda eng zaif qo'riqlanayotgan darvozalar sonini chop eting.
Tushuntirish:
So‘rovlardan oldin darvozalarning qo‘riqlanish holati [0,0,0,0,0,0,0,0] bo’lgan. (0 - hech qaysi qo‘riqchi darvozani qo‘riqlamasligini anglatadi).
Hech qaysi darvoza qo‘riqlanmaganligi sababli 1-so‘rov uchun javob 8.
2-so‘rovdan so‘ng darvozalarning qo‘riqlanish holati [3,3,3,3,0,0,0,0] bo‘ladi.
Endi eng zaif qo‘riqlanayotgan darvozlalar [5…8] o‘rindagi darvozalardir. Shuning uchun ham 3-so‘rovga javob 4.
6-so‘rovdan so‘ng darvozalarning qo‘riqlanish holati [3,3,5,5,6,6,6,9] bo‘ladi.
Endi [1…2] o‘rindagi darvozalar eng zaif qo‘riqlangandir. Shuning uchun ham 7-so‘rovga javob 2.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
8 9 2 1 1 4 3 2 1 5 7 6 1 3 4 5 1 8 8 9 2 1 1 8 20 2 |
8 4 2 8 |